Minimum Phase and Linear Phase Filters

Electronic filters have been around for over a century, the earliest passive designs employing resistors, capacitors and inductors used in telegraph, telephone and radio applications. Many configurations have been developed, but all hardware designs have a common limitation – any filter made with electrical components will introduce “phase shift”, the magnitude depending on the filter design, the frequencies involved, and the “steepness” of the filter. Actually, the term phase shift in this case means that different frequencies are delayed by very short, but different times, so that the phase shift varies in a nonlinear manner with frequency. All analog filter designs (which are called minimum phase filters) yield variable phase shifting with frequency. In addition, due to the resonant circuitry of a hardware filter, analog designs may create ringing after an input signal stops. Some people may think this is all a “bad” thing, but in fact, it’s what we’ve heard in numerous recordings made over many decades, all the great music of the 60’s, 70’s, 80’s, 90’s – and many classic analog EQ hardware units using minimum phase designs are still sought-after today.

An alternate filter design concept is the linear phase filter where the phase response is a linear function of input frequency which results in all frequency components of the input signal being shifted in time by the same constant amount. This results in no relative phase shift across the frequency range. Such a design has been known theoretically for a long time, but has one rather significant unrealistic requirement – it requires negative time! The filter must respond to the input signal before the input signal occurs! As a result there are no hardware linear phase EQs available!

However, digital signal processing introduced the concept of latency years ago that essentially allows using negative time in audio signal processing. The use of latency enables such things as “look-ahead” compression which allows a compressor to see a signal in advance of it being processed. In a sense using latency enables a response to “occur” before the stimulus! So linear phase filters can actually be implemented in software.

While there are arguments about the “smearing” of sound using minimum phase filters being a problem, others would call this effect coloration of the sound. What might this mean in terms of distorting audio? Applying the same low pass filter to a square wave, a waveform with high levels of harmonics, we can show how both minimum phase and linear phase filters affect the output.

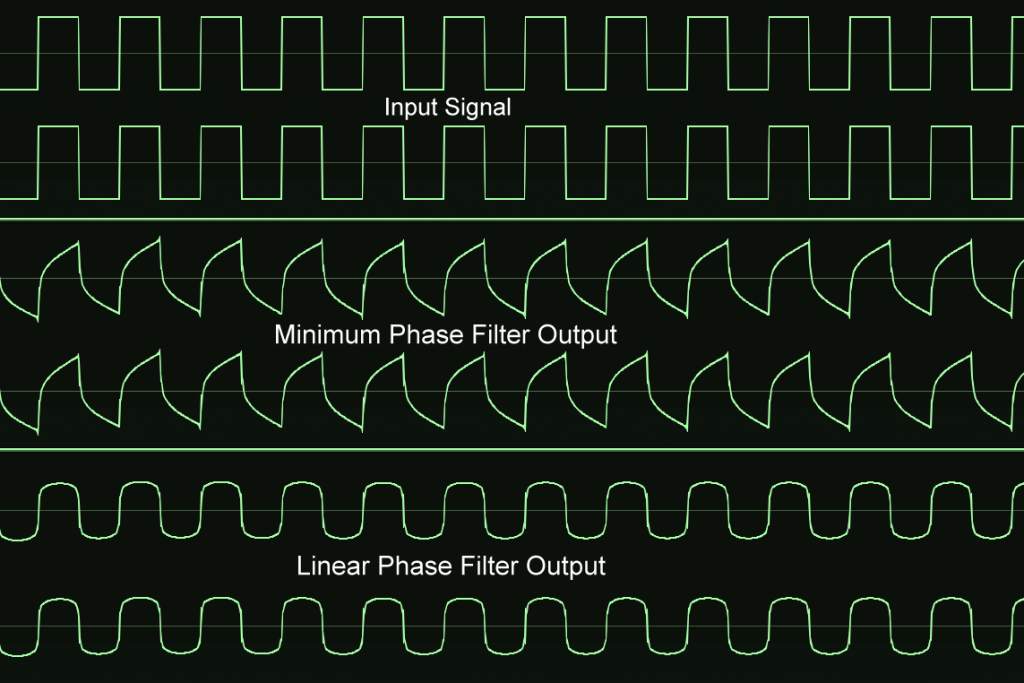
The above plots shows there is a dramatic difference in the resulting waveforms between minimum and linear phase designs when filtering a square-wave with exactly the same EQ parameters. This difference is due strictly to phase differences and certainly looks like significant coloration, so you might think the difference in sound would be obvious. However, the two resulting wave-forms sound exactly alike! This is because human hearing is like a spectrum analyzer and both of these output wave-forms have exactly the same spectra as can be seen in these plots using Voxengo’s SPAN (https://www.voxengo.com/). You can also see at the bottom of the SPAN window that the peak level of the minimum phase waveform is 1.4 dB higher than the more rounded looking linear phase waveform, which is not too surprising.

Our hearing does not detect phase effects directly, so using a minimum phase EQ on a track or full mix is not going to create any audible distortion in itself. However, there are situations where this “coloration” can cause undesirable results: when processing several tracks or subgroups that include some of the same sounds, you may encounter significant comb-filtering between the tracks when different minimum phase EQ settings are used on different tracks.

These screens show the same sine-wave frequency sweep with notch filters at 500 Hz and 1 kHz in the top two pair of traces – the bottom plots are the sum of these signals. The minimum phase filter on the left creates four partial phase cancellations shown by the arrows while the linear phase filter yields only the expected -6 dB dips at 500 Hz and 1 kHz. As you can see, linear phase filters don’t alter phase relationships, so they won’t create comb-filtering and may be a better choice in these situations.

But linear phase filters are not the answer for all applications and bring their own issues to the table. A linear phase filter requires latency, so may not be suitable for applications like live sound or tracking. This is not a problem for mixing and mastering, so you may think all is well. However, a linear phase filter presents one additional issue in the “negative time region”, called pre-ringing. Just as the maths showed back when a linear phase filter was only a theoretical concept, there is a “reflection” of the signal before it actually occurs! This can cause a “smearing” of sharp percussive sounds that is clearly audible in some cases, especially with steep filter slopes and high EQ boosts. As the saying goes, there is no free lunch!

Stranger than fiction! The top input waveform is a brief nine-cycle square wave burst – minimum and linear phase filtering responses using the same EQ settings are shown below. In this example a steep EQ curve with high Q factor was used to accentuate ringing – note the post-ringing for minimum phase lasts twice as long as for linear phase, but linear phase EQ starts ringing before the square wave input even starts!

So we have two basic filter designs, minimum phase available both with hardware and software designs, and linear phase available only in software. DynOne 3 use specially designed linear phase filters that minimize pre-ringing and eliminate any phase cancellation issues. DynOne also offers a very low latency option that uses a minimum phase design if you need a low processing latency and low CPU usage. This setting is ideal for use in Broadcast or Live mixing scenarios. But for the most precise results, the Ultra Quality and Master Quality modes in DynOne 3 use specially designed linear crossover filters that result in zero negative summing with no audible artifacts around the crossover frequencies.

Written by Dennis J Wilkins.

← Back